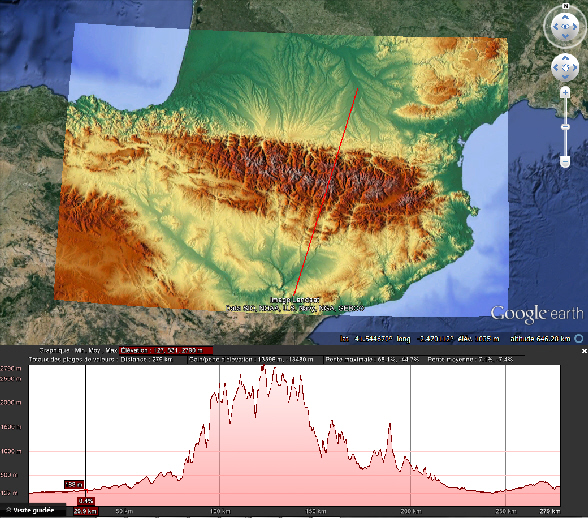
Il faut ensuite déterminer l'altitude en fonction de la distance parcourue sur l'itinéraire.
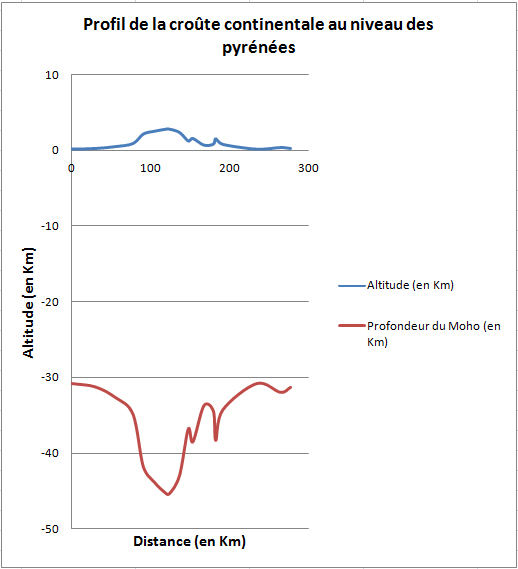
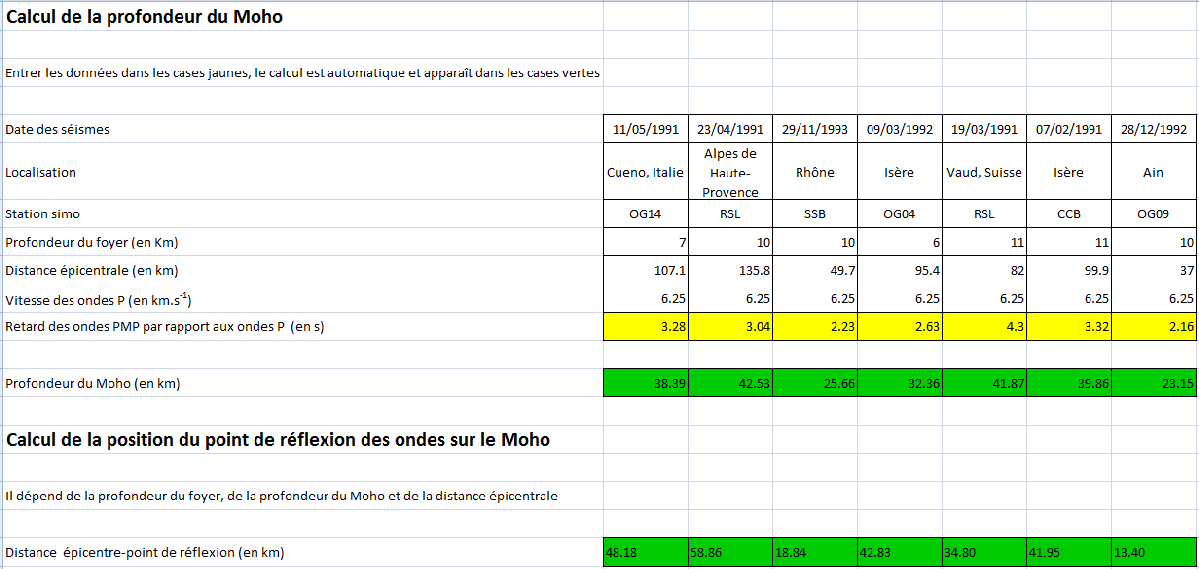
Il ne reste plus qu'à remplir le tableur et afficher le profil de la croûte continentale ainsi obtenue :
(Ec0 x ρc) + (Em0 x ρm) = (Ec1 x ρc) + (Em1 x ρm)
(Ec0 x ρc) + (Em0 x ρm) = ρc x (Ec0 + h1 + r1) + ρm x (Em0 - r1)
(ρc x h1) + (ρc x r1) - (ρm x r1) = 0
r1 x (ρc - ρm) = - (ρc x h1)
r1 = - (ρc x h1) / (ρc - ρm)
Sur le logiciel Google Earth, nous pouvons tracer un itinéraire à travers une chaîne de montagne et afficher son profil d'élévation (il est aussi possible, comme présenté ici, de rajouter la carte du relief) :
Nous constatons une variation de la profondeur du Moho : celle-ci augmente avec l'altitude. Il ya bien présence d'une racine crustale, comme le prévoit le modèle d'Airy.
5- Le calcul théorique de la profondeur du Moho en fonction de l'altitude :
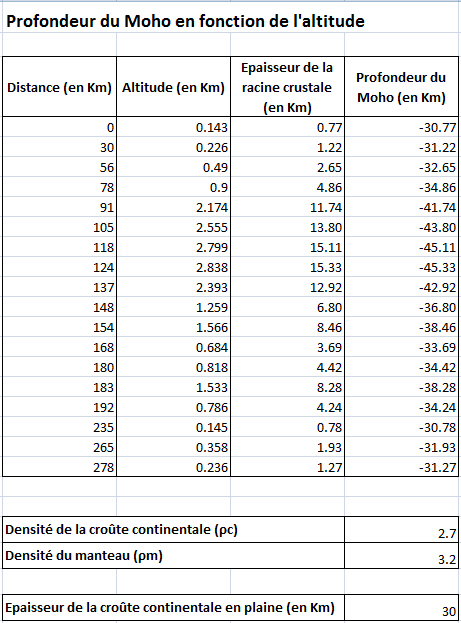
Activité : à l'aide d'un tableur, déterminer l'épaisseur de la racine crustale et donc la profondeur du Moho en fonction de l'altitude.
Principe: nous appliquerons le modèle d'Airy. Sachant que la densité de la croûte et du manteau sont respectivement 2.7 et 3.2 et qu' au-dessus de la surface de compensation, toutes les colonnes de roches de même section doivent avoir la même masse :
(d'après http://www2.ac-lyon.fr/enseigne/biologie/spip.php?article176)
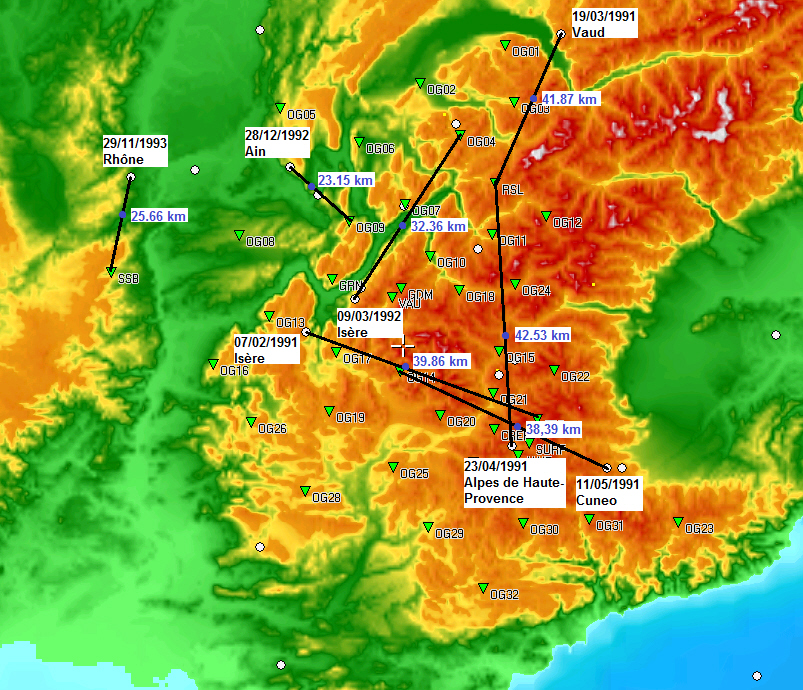
Utilisation de Sismolog :
- Lancer le logiciel Sismolog.
- Zoomer sur les Alpes.
- Afficher les stations (Affichage --> Stations) et les séismes (Séismes --> Base de données).
- Ouvrir les données sismiques (Fenêtre --> Traces) et choisir un séisme (les séismes choisis sont les plus exploitables).
- Décocher les stations non étudiées.
- Afficher les temps d'arrivée des ondes P et S (Solutions --> Voir les temps de références).
- Déterminer la profondeur du séisme (Localiser --> Référence).
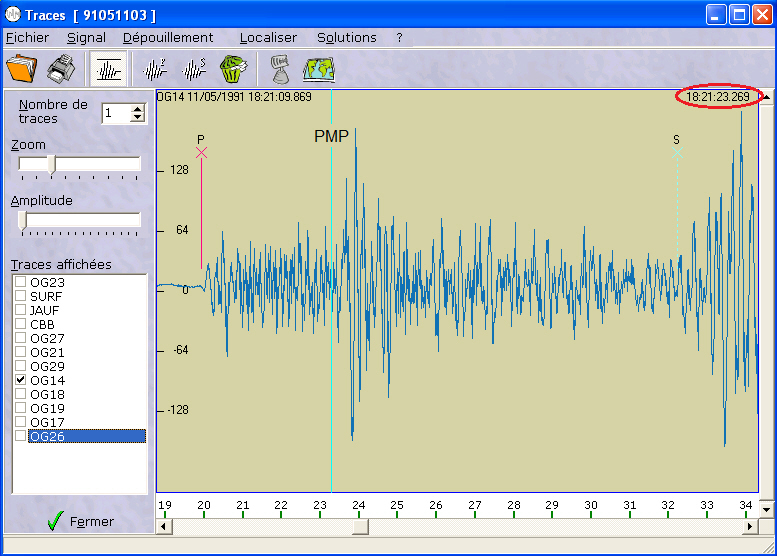
- Zoomer et déterminer le temps d'arrivée (en haut, à droite) des ondes P et PMP :
Après avoir mesuré la masse m (en g) et le volume V (en cm3) des échantillons de roche, il ne reste plus qu'à calculer leur masse volumique mV (en g.cm-3) : mV = m / V
Remarque : on peut aussi utiliser la densité d (sans unité) des roches. Dans ce cas la il suffit de diviser le résultat obtenu par la masse volumique de l'eau (mV eau = 1 g.cm-3).
La masse volumique du granite et du gneiss sont en moyenne de 2.7 g.cm-3 et la masse volumique de la péridotite est de 3.3 g.cm-3.
Nous pouvons en déduire que la croûte repose sur des roches (la péridotite) de masse volumique plus importante.
4- Le calcul de la profondeur du Moho grâce au données sismiques (d'après Eric Lecoix) :
Activité : étudier les données sismiques de Sismolog pour calculer la profondeur du Moho.
Principe : la différence de temps d'arrivée des ondes P et des ondes PMP (réfléchies par le Moho) va nous permettre de calculer la profondeur du Moho au niveau du point de réflexion des ondes P :
Dans ce modèle aussi, toutes les colonnes de même section ont bien la même masse : mA = mB
Ici aussi, les anomalies magnétiques négatives sont expliqués par une densité plus faible lorsque le relief s'élève. En effet, si l'on considère les colonnes A et B, il y a plus d'éléments de faible densité dans la colonne A que dans la colonne B donc, au-dessus de la surface de compensation, la densité moyenne de la colonne A est inférieure à celle de la colonne B.
Les activités suivantes auront pour but de déterminer le bon modèle.
3- Le calcul de la densité des roches de la croûte et du manteau :
Activité : à l'aide d'une balance et d'une éprouvette, déterminer la masse volumique de différents échantillons roches : granite, gneiss et péridotite.
Dans ce modèle, toutes les colonnes de même section ont bien la même masse : mA = mB
De plus, les anomalies magnétiques négatives sont expliqués par une densité plus faible lorsque le relief s'élève.
Le modèle d'Airy :
Contrairement au modèle de Pratt, le modèle d'Airy suppose que les roches de la croûte ont toutes la même masse volumique et qu'elles reposent sur des roches de masse volumique plus importante. Les variations d'altitude seraient compensées par des variations d'enfoncement de la base de la croûte en profondeur :
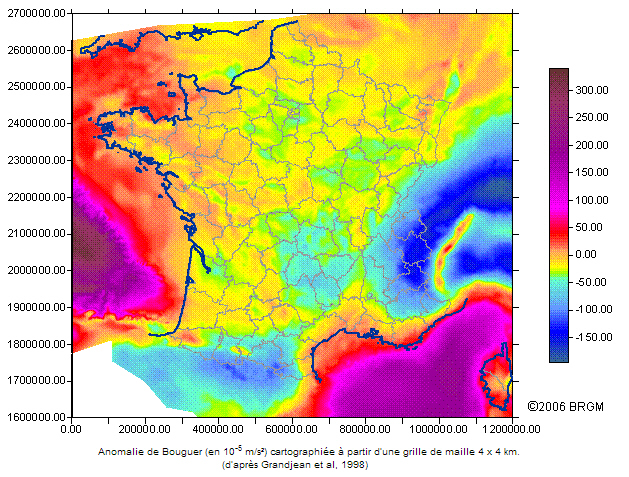
Nous remarquons une corrélation entre les anomalies de Bouguer et l'altitude des reliefs. En effet, plus les reliefs sont élevés, plus les anomalies de Bouguer sont négatives, et donc plus la pesanteur mesurée est faible par rapport à la pesanteur théorique.
Or, nous aurions pu penser que l'excédant de masse apporté par une montagne aurait l'effet inverse et que la pesanteur mesurée serait plus importante que la pesanteur théorique.
Pour expliquer l'origine de ces anomalies gravimétriques négatives, les géophysiciens, qui ont fait le même constat, en ont déduit que l'excédant de masse du aux chaînes de montagnes devait être compensé en profondeur par un déficit de masse. Cette compensation se ferait au-dessus d'une surface virtuelle appelée "surface de compensation". Ainsi, au-dessus de cette surface de compensation, toutes les colonnes de roches de même section devraient avoir la même masse, permettant l'équilibre de la lithosphère sur l'asthénosphère : c'est la théorie de l'isostasie.
Pour rendre compte de ce phénomène, deux géodésiens, Henry Pratt et George Biddell Airy, ont élaboré deux modèles.
2- La modélisation analogique et la comparaison des modèles de Pratt et d'Airy :
Activité : avec l'aide hypothèses émises par Pratt et Airy, réaliser une modélisation analogique des modèles de Pratt et d'Airy. Pour ce faire, diverses maquettes sont disponibles dans le commerce. Leur fabrication est aussi envisageable.
a- Le modèle de Pratt :
Le modèle de Pratt suppose que, au-dessus d'une surface de compensation située à plus de 100 km de profondeur, les variations d'altitude sont dues à des variations latérales de masse volumique :
1- L'étude des données gravimétriques :
Activité : Comparaison relief / Anomalies gravimétriques (anomalies de Bouguer)
La gravimétrie est l'étude et la mesure de la pesanteur terrestre. Celle-ci est en moyenne de g = 9.81 m.s-2 (= 9.81 N.kg-1).
Grâce à des gravimètres très précis, il est possible de mesurer la valeur de g. Il existe une variation entre la valeur mesurée et la valeur théorique de g. Ainsi, nous appelons anomalie de Bouguer la différence entre la pesanteur mesurée et la pesanteur théorique.
En 1950, le B.R.G.G.M. (Bureau de Recherches Géologiques, Géophysiques et Minières) s'est vu confié l'établissement de la carte gravimétrique de la France, ce qui a permis d'établir par la suite la carte des anomalies de Bouguer :
Principe :
Il s'agit ici d'aborder la notion d'isostasie par le biais de différentes activités :
- L'étude des données gravimétriques.
- La modélisation analogique et la comparaison des modèles de Pratt et d'Airy.
- Le calcul de la densité des roches de la croûte et du manteau.
- Le calcul de la profondeur du Moho grâce au données sismiques.
- Le calcul théorique de la profondeur du Moho en fonction de l'altitude.
L'ISOSTASIE
Définition :
Isostasie : équilibre lithostatique des enveloppes superficielles réalisé à partir d'une certaine profondeur, qu'il est possible de matérialiser par une surface théorique dite de compensation ou d'égale pression (d'après Géologie tout-en-un . 1er et 2e années BCPST, Pierre Peycru).